[最も好ましい] ƒr[ƒ€ƒX ƒƒ“ƒY ƒR[ƒf 102134-X=r-h/y solve for r

Nov 13, 19 · \x = r\cos \theta \hspace{05in}y = r\sin \theta \hspace{05in}{r^2} = {x^2} {y^2}\ We are now ready to write down a formula for the double integral in terms of polar coordinatesTo show f(x;y) is a valid joint pdf we must check that it is positive (which it clearly is) and that the total probability is 1 1 1 1 1 Total probability = 1 Z 4xydxdy = 2x2y dy = 2ydy = 1 QED 0 0 Z 0 Z 0 Z 0 The event A is just the upperlefthand quadrant Because the density is not constant weY Mathematical Properties of Functional Dependencies De nition 4 Let F be a set of FDs on scheme R and f be another FD on R Then, F implies f, denoted by F j= f, if every relation

Let F Mathbb R Mathbb R 3 Be Defined By F X Langle 8x 6x 8x Rangle Is F A Linear Transformation Mathematics Stack Exchange

X=r-h/y solve for r

X=r-h/y solve for r-Make appropriate changes of variables in the integral ∬ R 4 (x − y) 2 d y d x, ∬ R 4 (x − y) 2 d y d x, where R R is the trapezoid bounded by the lines x − y = 2, x − y = 4, x = 0, and y = 0 x − y = 2, x − y = 4, x = 0, and y = 0Exercise 1C24 A function f R !

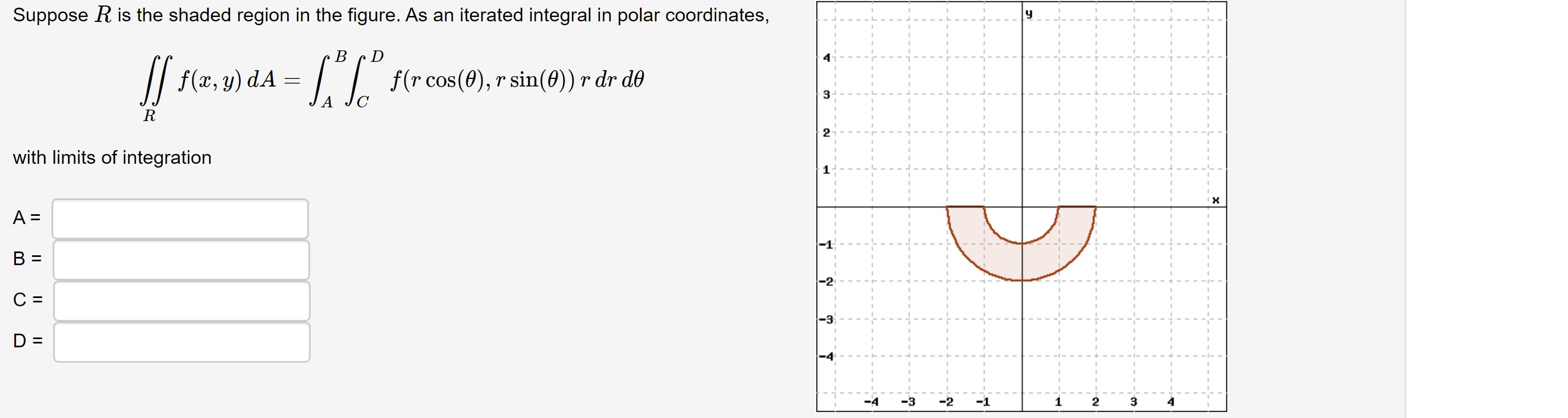
Answered Suppose R Is The Shaded Region In The Bartleby

Solution (a) x = 2sint, y = 3cost =) sint = x=2;Dec 21,  · For \(x, y \in A\), \(x\ R\ y\) if and only if \(x\) and \(y\) have the same number of digits Prove that \(R\) is an equivalence relation on the set \(A\) and determine all of the distinct equivalence classes determined by \(R\)If f (x y) = f (x) f (y) ∀ x, y ∈ R and f ′ (0) = 5, f (2) = 6, then f ′ (2) View solution If x = A cos 4 t B sin 4 t , then d t 2 d 2 x is equal to

Apr 04, 18 · Let f(x, y) be a periodic function which satisfies the condition f(x, y) = f(2x 2y, 2y 2x) ∀x, y ∈ R asked Dec 2, 19 in Sets, relations and functions by RiteshBharti ( 538k points) setsR is called odd if f( x) = f(x) for all x 2R Let U e denote the set of realvalued even functions on R and let U o denote the set of realvalued odd functions on R Show that RR = U e U o Proof 1 First, we check that U e and U o areFor all x,y∈ Rn, α ∈ R The notation L R n → R m is used to indicate that the input vectors come from the set R n (= domainof L) and the output vectors are in the set R m (=

Question Show that M2,2, the set of all 2×2 matrices, is a vector space Solution We need to check each and every axiom of a vector space to know that it is in fact a vector space A1 Let · a1,1 a1,2 a2,1 a2,2 b1,1 b1,2 b2,1 b2,2 ∈ M2,2ThenJan 28,  · Transcript Ex 12, 12 Let f R → R be defined as f(x) = 3x Choose the correct answer (A) f is oneone ,onto (B) f is manyone onto f is oneone but not onto (D) f is neither oneone nor onto f(x) = 3x Checking oneone f (x1) = 3x1 f (x2) = 3x2 Putting f(x1) = f(x2) 3x1 = 3 x2 Rough Oneone Steps 18 Let f(x,y) R2 R and g(x,y) R2 R be two functions from C(R2) satisfying the CauchyRiemann conditions fr(x, y) = gy(2,y) and fy(x, y) = 9x(x,y) = (a) (5 points) Show that f(x, y) is a harmonic function, that is, fxx(xc, y)fyy(x, y) O for all (x, y) = RP

Diracc Sec 6 1

Let F 0 1 Rarr R Be Such That F Xy F X F Y For All X Y In 0 1 And F 0 Ne 0 If Youtube

R is called even if f( x) = f(x) for all x 2R A function f R !Curl The second operation on a vector field that we examine is the curl, which measures the extent of rotation of the field about a point Suppose that F represents the velocity field of a fluid Then, the curl of F at point P is a vector that measures the tendency of particles near P to rotate about the axis that points in the direction of this vector The magnitude of the curl vector at PSCRABBLE® is a registered trademark All intellectual property rights in and to the game are owned in the USA and Canada by Hasbro Inc, and throughout the rest of the world by JW Spear & Sons Limited of Maidenhead, Berkshire, England, a subsidiary of Mattel Inc Mattel and Spear are not affiliated with Hasbro

Ex 1 2 7 State Whether One One Onto Or Bijective Class 12

Asymptote

I am using R 343, and plotting the following function x = rnorm(5000,,30) cdf_1 <Convex functions Definition f Rn → R is convex if dom f is a convex set and f(θx (1−θ)y) ≤ θf (x) (1−θ)f (y) for all x,y ∈ dom f, and θ ∈ 0,1 f is concave if −f is convex f is strictly convex if dom f is convex and f(θx (1−θ)y) < θf (x) (1−θ)f (y)F(rxsy)=rf(x)sf(y)forallx,y∈ Mandr,s∈ R Equivalently, f ( x y )= f ( x ) f ( y )and f ( rx )= rf ( x )forall x,y∈ M and r∈ R The kernel ofahomomorphism f isker f = {x∈ M f ( x )=0 } ,andthe image of f

15 2 Double Integrals Over General Regions Mathematics Libretexts

Relations And Functions Class 12 Maths Chapter 1 Toppers Bulletin

Let a radius of length r sweep out an angle θ in standard position, and let its endpoint have coördinates (x, y) The question is How shall we now define the six trigonometric functions of θ?$$ F Rx \otimes Ry \rightarrow Rx,y, r \otimes s \mapsto rs $$ For the other direction, define $$ G Rx,y \rightarrow Rx\otimes Ry, x^i y^j \mapsto (x^i \otimes y^j) $$2 Suppose that f R→ R3 and g R3 → Rare defined by f(t) = (t,t2,t3), g(x,y,z) = x2eyz, and h= g f R→ Ris their composition (a) Use the chain rule to compute h′(1) (b) Find h(t) and compute h′(1) directly Solution

Week 6

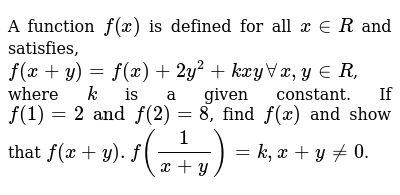
A Function F X Is Defined For All X In R And Satisfies F X

An example algorithm R U R' U R U2 R' U Explained R U R' U R U2 R' U There is another commonly used notation where the uppercase means a clockwise and lowercase means a counterclockwise turn, but this is not the official version because for other twisty puzzles the lowercase letter marks a different thing eg R U r U R U2 r U Sometimes they mark the inverse rotations with the capital3sinti (c) See the graph above 26 Find parametric equations for the tangentChapter8 IntroducingAlgebraic Geometry (CommutativeAlgebra2) WewilldevelopenoughgeometrytoallowanappreciationoftheHilbertNullstellensatz

Consider A Differentiable Function F R R For Which F 0 Ln2

Functions In R Programming With Example

Grad f f f f( ) = x y z, , div curl( )( ) = 0 Verify the given identity Assume conti nuity of all partial derivatives F ( ) ( ) ( ) ( ) Let , , , , , , , ,P x y z Q x y z R x y z curl x y z P Q R = ∂ ∂ ∂ = ∇× = ∂ ∂ ∂ F i j k F F curl R Q P R Q P(F) = − − −y z z x x y, ,, ,( ) since mixed partial derivatives are equalNote that F is defined on {(x,y) ∈ R (x,y) 6= (0 ,0)} (a) Evaluate R C1 F· dr, where C1 is the circle x2 y2 = 1, oriented counterclockwise Solution A vector equation of C1 is given by r(t) = hcost,sinti, 0 ≤ t ≤ 2πStack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

Let F Be A Differentiable Real Valued Function Satisfying F X Y F X F 2y 6xy X 2y For All X Y Maths Continuity And Differentiability Meritnation Com

Lesson18 Double Integrals Over Rectangles Slides

Sep 25, 18 · Hence, if f(x1) = f(x2) , x1 = x2 ∴ function f is oneone Onto f(x) = 2x Let f(x) = y, , such that y ∈ R 2x = y x = 𝑦﷮2﷯ Since y is a real number, Hence 𝑦﷮2﷯ will also be a real number So, x will also be a real number, ie, x ∈ R Hence, f is ontoNov 10,  · CHKDSK /F /R vs CHKDSK /R /F Windows 10 If you want to repair a corrupted hard drive and try to run both chkdsk /f and /r switches in Windows 10, you can type chkdsk /f /r or chkdsk /r /f command in CMD in Windows 10 There no much difference between chkdsk /f /r and chkdsk /r /fMar 23, 21 · chkdsk volume /f /v /r /x /i /c If used without parameters, CHKDSK displays only the volume's status and does not fix any errors If used with the /f, /r, /x

Integrating Functions Of Several Variables

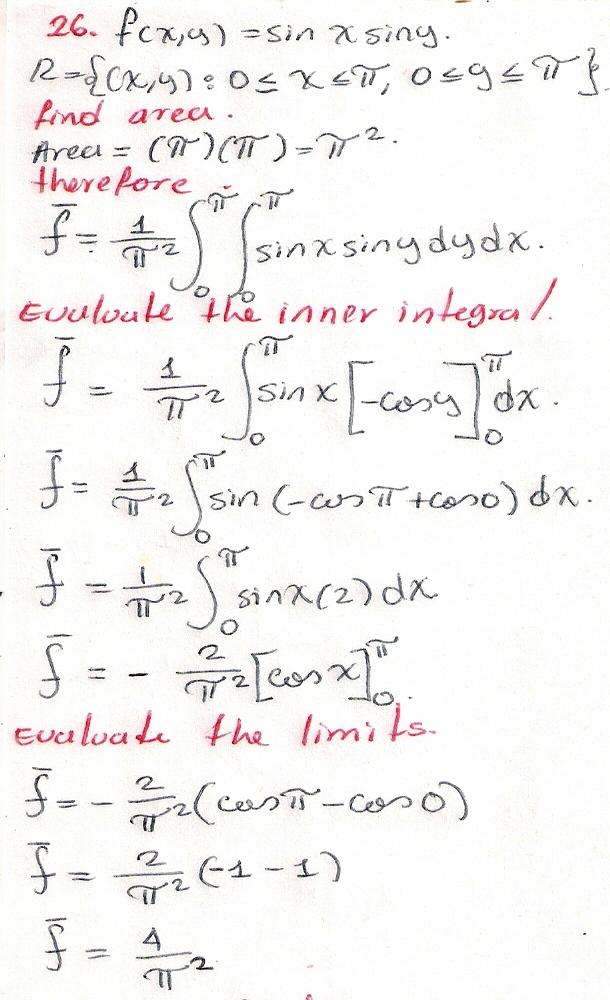
Compute The Average Value Of The Following Functions Over The Region R F X Y Sin X Sin Y R X Y 0 Leq X Leq Pi 0 Leq

De nition 65 A function fisonetooneorinjectiveif and only if f(x) = f(y) implies x= yfor all x;yin the domain Xof f Formally 8x;y2X(f(x) = f(y) !x= y) In words, this says that all elements in the domain of f have di erent images Example 98 Consider the function f R !R, f(x) = 4x 1 We want to know whether each element of R has a diRf(x,y)dA where f(x,y)=3x3 and R=4,8 Expert Answer 100% (1 rating) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculatorAnd cost = y=3 So sin2 tcos2 t = x2 4 y2 9 = 1 The curve is an ellipse with center at (0;0) and the major axis along the yaxis x ( /3) (p/3) p/2 r y r −3 −2 0 2 ( 3 , 3/2) t=0 3 t= p (b) r0(t) = h2cost;

If F R R Satisfies F X Y F X F Y For All X Sarthaks Econnect Largest Online Education Community

Solved A Function T R N Rightarrow R Is Called A Linear Chegg Com

This lesson examines the properties of the quadratic function in intercept or factored form y = a(x r)(x s) This is one of a series of math video lesson2 (a) Define uniform continuity on R for a function f R → R (b) Suppose that f,g R → R are uniformly continuous on R (i) Prove that f g is uniformly continuous on R (ii) Give an example to show that fg need not be uniformly continuous on R Solution • (a) A function f R → R is uniformly continuous if for every ϵ > 0 there exists δ > 0 such that f(x)−f(y) < ϵ for all xCurves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2"That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cg Example When we say \the curve x 2 y = 1," we really mean \The

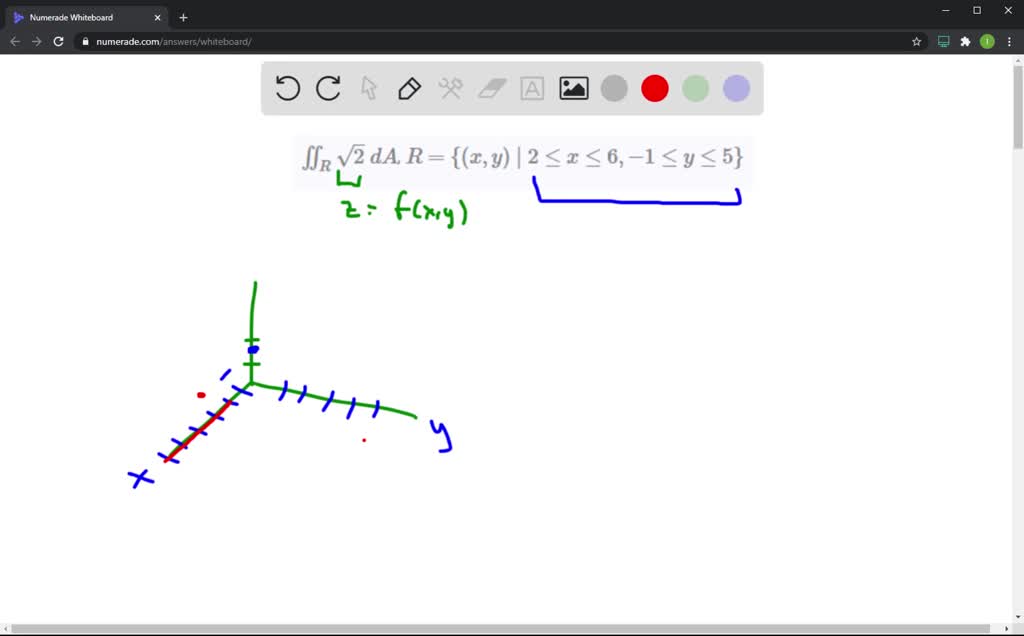
Solved Evaluate The Double Integral By First Iden

Euler Method To Solve Ordinary Differential Equations With R Sandipanweb

If f(x) be a continuous function for all real values of x and satisfies x 2 {f (x) − 2} x 2 3 − 3 − 3 f (x) = 0;(a) f(x,y,z) = 3x3y2z3 (b) f(x,y,z) = √ xz y (c) f(x,y,z) = p x2 y2 z2 (d) f(x,y,z) = 1 p x2 y2 z2 Quiz Choose the Laplacian of f(r) = 1 rn where r = p x2 y2 z2 (a) − 1 rn2 (b) n rn2 (c) n(n−1) rn2 (d) n(n5) rn2 The equation ∇2f = 0 is called Laplace's equation This is an important equation in science From the aboveEcdf(x) plot(cdf_1, xlabs="x0", ylabs="y0") This gives me the following plot Now, the plot

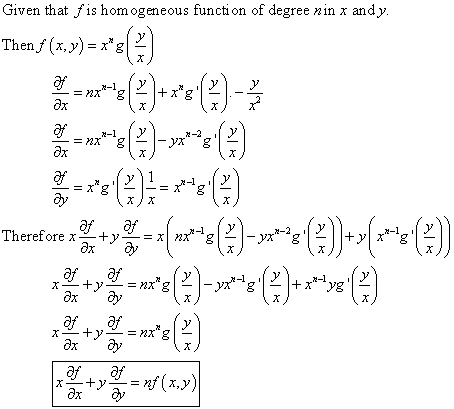
A Function F R 2 Rightarrow R Is Called Homogeneous Of Degree N If It Satisfies F Tx Ty T N F X Y For Example G X Y Xy 2 Is Homogeneous Of Degree 3

Ug Math

F is the symbol of the function The R on the left is the domain of the function It is the range of values from which you chose an input value for your function The R on the right side of the arrow is the codomain , the set from which function cSearch through our comprehensive database of words using our advanced word finder and unscramblerWe will take our cue from the first quadrant In that quadrant, a radius r will terminate at a point (x, y) Those coördinates define a right triangle

Suppose R Is The Shaded Region In The Figure And F X Y Is A Continuous Function On R Find The Limits Of Integration For The Following Iterated Integrals 3 A F X Y

1 Vytah

∀ x ϵ R Then find the value of f (3 ) View solution Let a 1 and a 2 be two values of a for which the expression f ( x , y ) = 2 x 2 3 x y y 2 a y 3 x 1 can be factorised into two linear factors then the productIf R = (x, y) x 2 y = 8 is a relation on N, write the range of R Advertisement Remove all ads Solution Show Solution The given relation on N is R = (x, y) x 2 y = 8 Let us find the different integral values of y for different integral values of x For x = 2, y = 3 For x = 4, y = 2 For x = 6, y = 11 TRUE or FALSE There is a function f R2!R such that @f @x = y and @f @y = x2 Solution FALSE (If there were such a function, then its mixed second partial derivatives would be @ 2f @y@x = 1 @f @x@y = 2x These functions are continuous and unequal, but by Clairaut's Theorem, if a function has continuous second partial derivatives then its

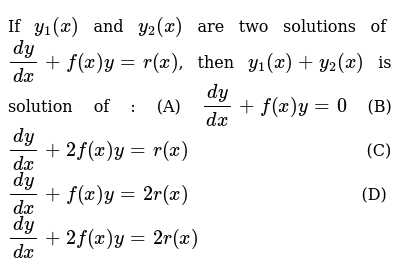
If Y 1 X And Y 2 X Are Two Solutions Of Dy Dx F X Y R

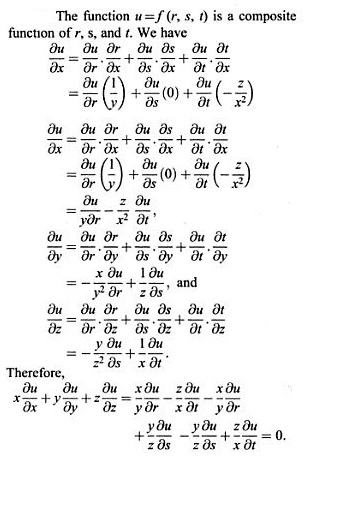
If U F R S T And R X Y S Y Z T Z X Show That Xdudx Ydudy Zdudz 0 Askiitians

Let f(x) = a nxn a n 1xn 1 a 1x a 0 and g(x) = b mxm b m 1xm 1 b 1x b 0 with f(x);g(x) 2Rx Let s= maxfn;mg Now, ˚ (f(x) g(x)) = ˚ ((a s b s)xs (a s 1 b s 1)x s 1 (a 1 b 1)x (a 0 b 0)) = ˚(a s b s)xs ˚(a 1 b 1)x ˚(a 0 b 0) where a i and b i are in R But ˚is a ring homomorphism from Rto Sso (i) it splits over2 days ago · ~s t q r m y f r x g z~ stqrmclquds 6 Follow Unfollow 3px arm (Slim) Background ~s t q r m y f r x g z~ stqrmclquds 6 Follow Unfollow Posted on Apr 25, 21 About 1 day ago 22 3 0 1 EYYYYYYYYYY WELCOME dis is a base for my lovely frxggie~ were making matching skins and i had an ideaIn this *improvised* video, I show that if is a function such that f(xy) = f(x)f(y) and f'(0) exists, then f must either be e^(cx) or the zero function It'

Calc 501 1000 By James Bardo Issuu

Answered Suppose R Is The Shaded Region In The Bartleby

Sep 10,  · Let the functioin 'f' be defined by f (x) = 5x² 2 ∀ x ∈ R, then 'f' is (a) onto function (b) oneone, onto function (c) oneone, into function (d) manyone into function Answer Answer (d) manyone into functionDe nition 3 Let R be a relation scheme and let X R and Y R Then X !Any function f(x 1, x 2, , x n) of n real variables can be considered as a function on R n (that is, with R n as its domain)The use of the real nspace, instead of several variables considered separately, can simplify notation and suggest reasonable definitionsConsider, for n = 2, a function composition of the following form = ((), ()),where functions g 1 and g 2 are continuous

Polar Coordinate System Wikipedia

If F X Is Continuous And Differentiable Function Such That F X Y F X F Y Xy X Y R And X 0 F H H 1 Then The Find

Y, a functional dependencyon scheme R, is valid if every legal instance r(R) satis es X !Theorem 36 Let F be any partition of the set S Define a relation on S by x R y iff there is a set in F which contains both x and y Then R is an equivalence relation and the equivalence classes of R are the sets of F Pf Since F is a partition, for each x in S there is one (and only one) set of F which contains xR has several operators to perform tasks including arithmetic, logical and bitwise operations In this article, you will learn about different R operators with the help of examples DataMentor Logo > x < c(2,8,3) > y < c(6,4,1) > xy 1 8 12 4 > x>y 1 FALSE TRUE TRUE

A Function F R Gt R Satisfy The Equation F X F Y F Xy X Y For All X Y In R And Youtube

Solved Let R X Y Z Define The Vector Field R 3 Chegg Com

Example Show that the function f R 3> R 2 defined by f(x, y, z) = (xy, yz) is not a linear transformation Solution To show a function is not a linear transformation, we just need to find an example that demonstrates the failure of one of the properties

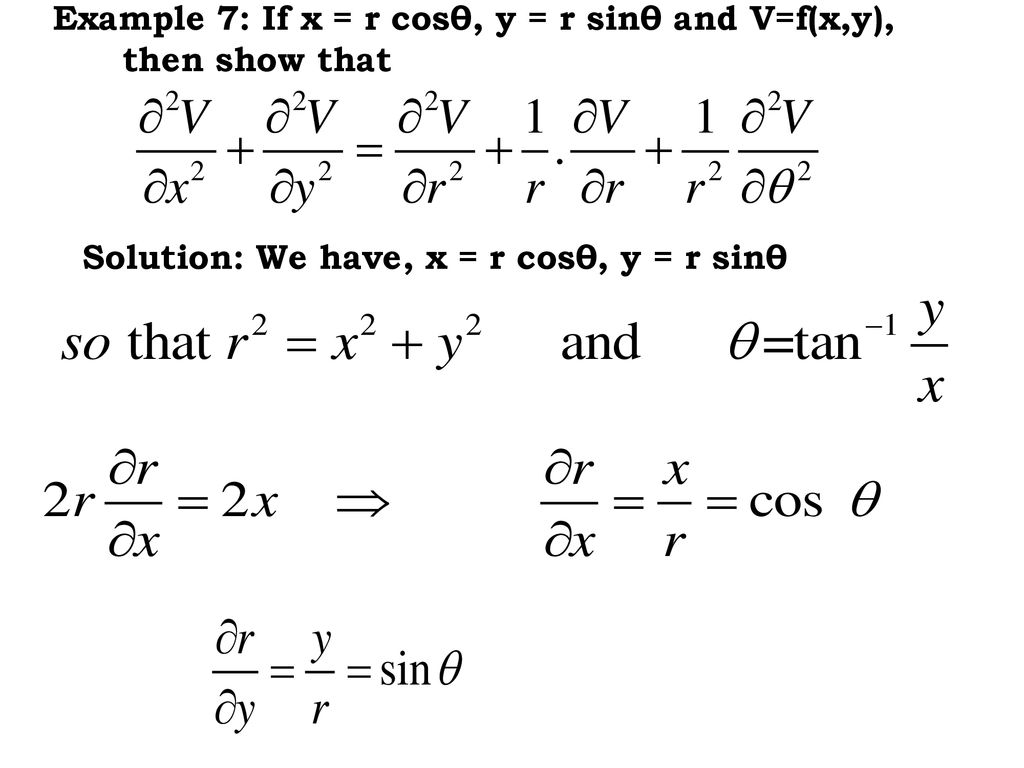
Differentiation Of Composite Function Let Z F X Y Possesses Continuous Partial Derivatives And Let X G T Y H T Possess Continuous Ppt Download

Let F Mathbb R Mathbb R 3 Be Defined By F X Langle 8x 6x 8x Rangle Is F A Linear Transformation Mathematics Stack Exchange

If F R To R Satisfies F X Y F X F Y For All X Y In R And F 1 7 Then Sum R 1 N F Youtube

A Function F R R Satisfies The Equation F X Y F X F Y For All Xy E R F X 0 Suppose That The Function Is Differentiable At X 0 And F 0 2 Prove That F X Mathematics Topperlearning Com A5z3qnjj

8 Points Suppose R Is The Shaded Region In The Figure And F X Y Is A Continuous Function On R Find The Limits Of Integration For The Following Iterated Integral Fx Y

Solved Problem 1 Let Us Define R Cr By R X Y X 0 Y Chegg Com

Relations And Functions Class 12 Maths Chapter 1 Toppers Bulletin

Find The Absolute Extrema Of The Function Over The Region R In Each Case R Contains The Boundaries Use A Computer Algebra System To Confirm Your Results F X Y 4xy

Parametric Equation 26 4 Sideway Output To

Calameo Ejercicios Resueltos De Funciones

Double Integrals

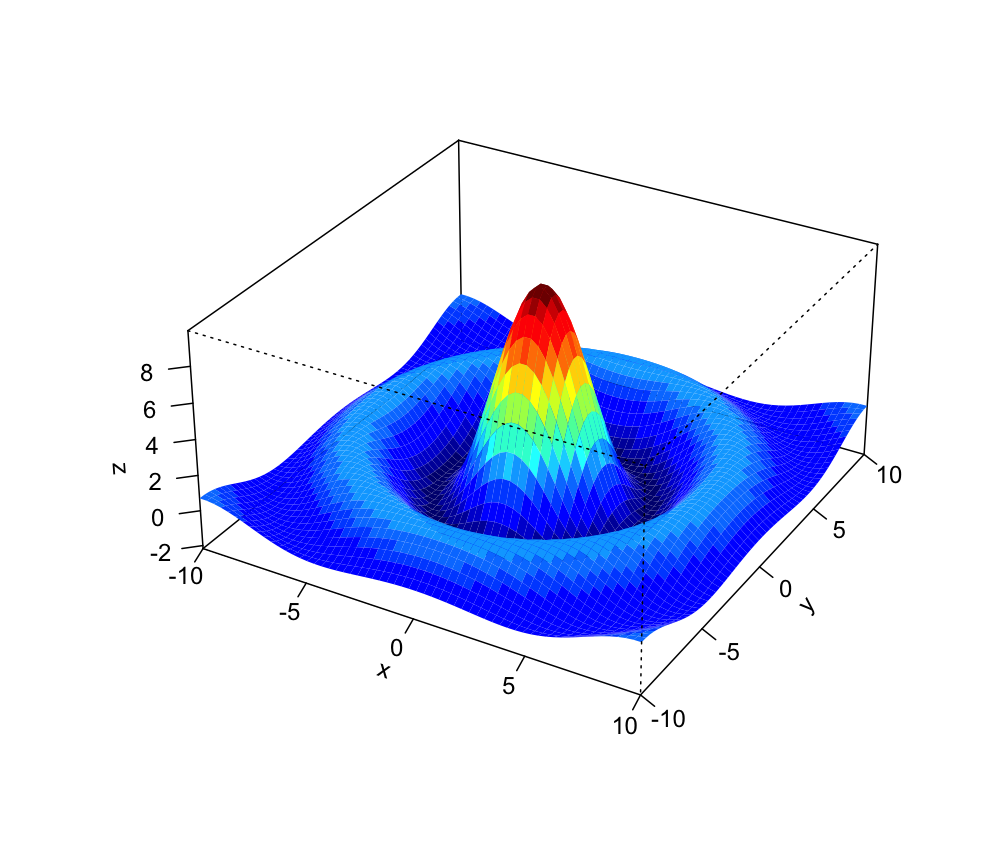
Perspective Plot With Colour Levels Persp3d Ga

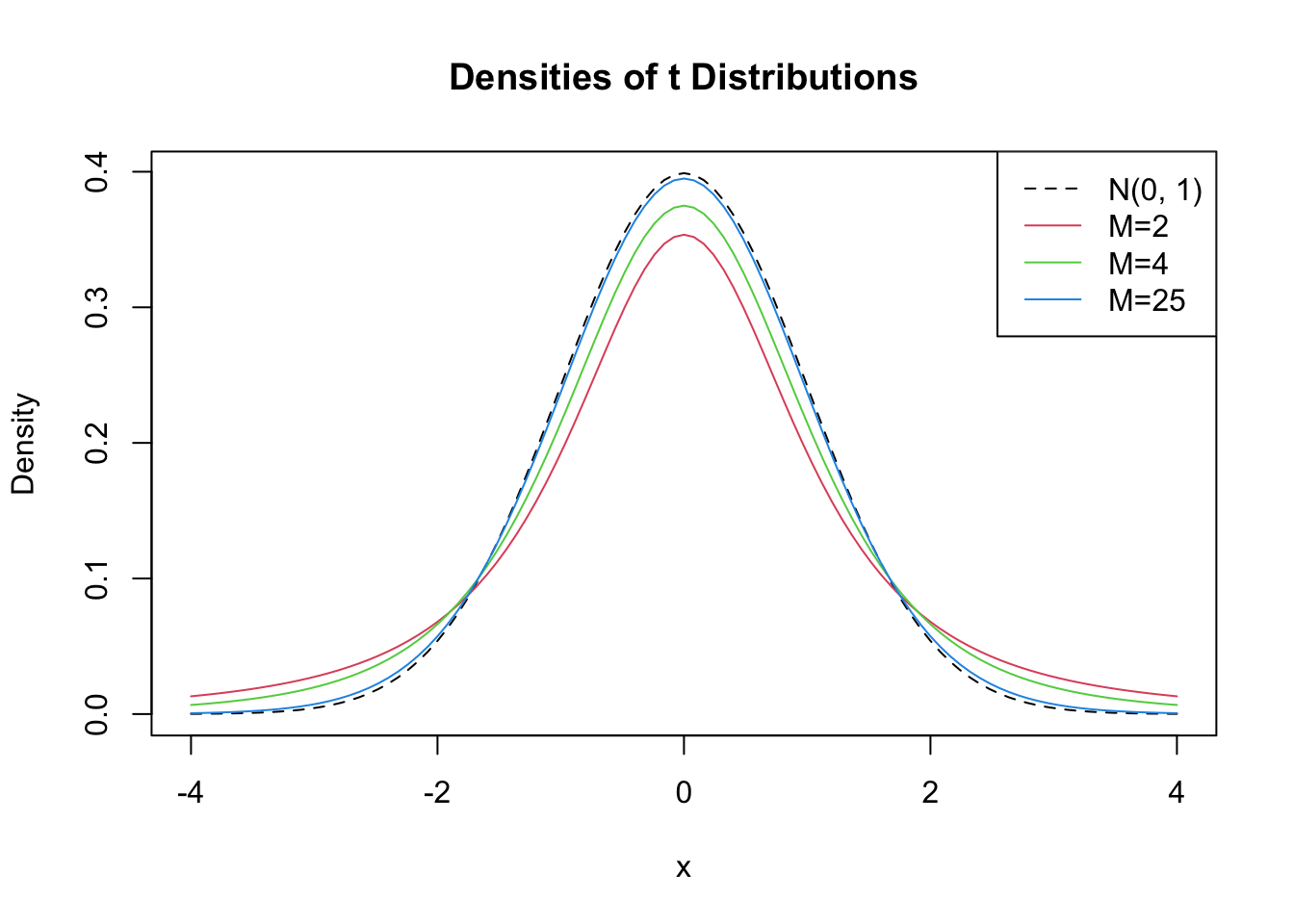
2 1 Random Variables And Probability Distributions Introduction To Econometrics With R

Ex 1 2 1 Class 12 Maths Show F X 1 X Is One One Onto Where R

Final Exam Review Pack

Let X And Y Be Subsets Of R The Set Of All Real Numbers The Function F X Y Defined By F X X 2 For X Epsilon X Is One

For X R Cos Theta Y R Sin Theta Gives Dr Dx Cos Theta Why See Pic For Detailed Equation Learnmath

Let F Be A Real Valued Function On Mathbb R 3 Satisfying Mathematics Stack Exchange

Derivatives Of Polar Functions

Solved Let F R 2 Rightarrow R 2 Be Defined By The Equati Chegg Com

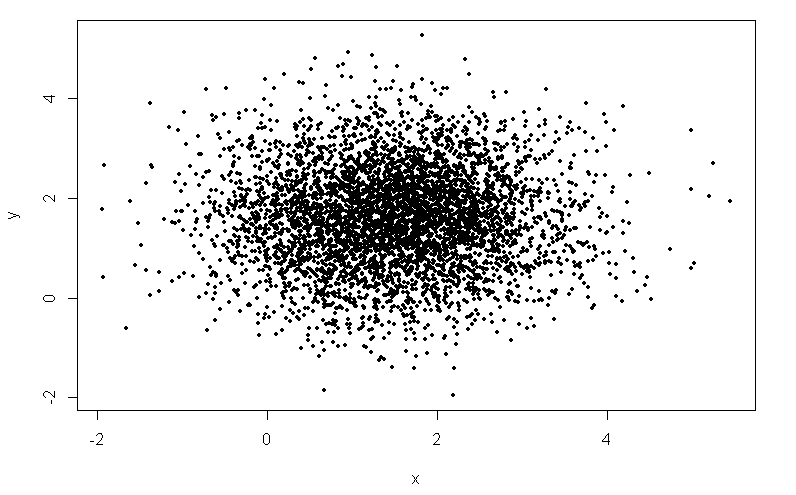
5 Ways To Do 2d Histograms In R R Bloggers

Fitting A Rational Function In R Using Ordinary Least Squares Regression Revolutions

Integration In Polar Coordinates

Answered 50 Polar Coordinates Suppose That We Bartleby

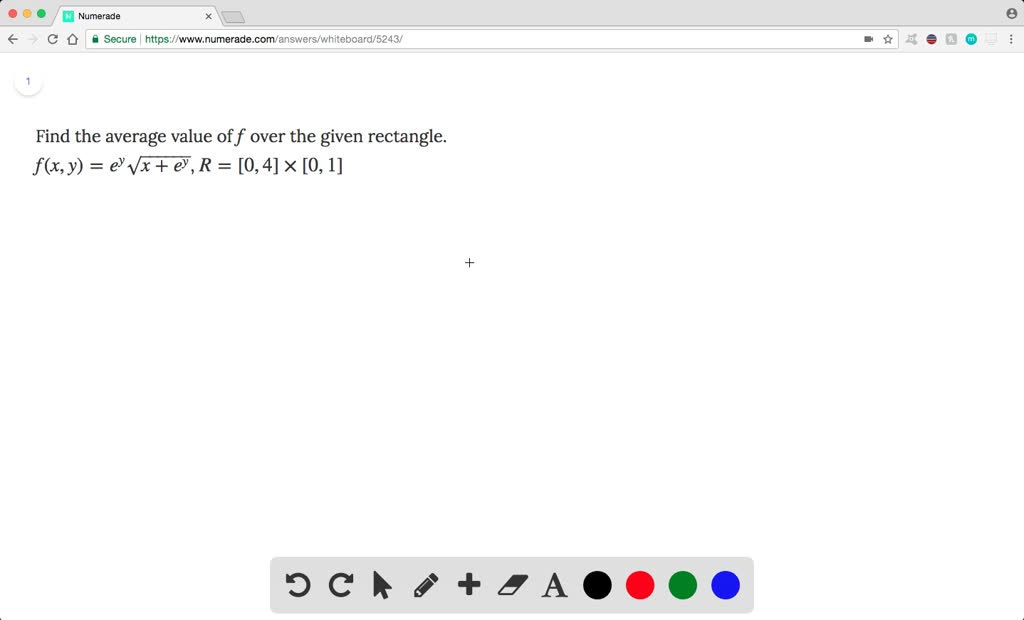
Solved Find The Average Value Of F Over The Given

A Function F R R Satifies The Equation F X Y F X F Y For All X Y R F X 0 Studyrankersonline

If 2f X F Xy F X Y For All X Y R F 1 0 And F 1 1 Then Sarthaks Econnect Largest Online Education Community

If F X Y F Xy For All X Y Belongs To R Then Prove That F Is A Constant Function

Calc 501 1000 By James Bardo Issuu

7 2 Double Integrals Over General Regions Mathematics Libretexts

What Does F R R This Signify For A Function F X Quora

Solved Please Help And Show Work Show Transcribed Image Text Suppose R 1 Answer Transtutors

Pdf On Generalized Derivations And Commutativity Of Rings

Incoming Term: formula for y=x, x.y.r. false angel lullaby, x=r-h/y solve for r, how to solve for y and x, how to find y equation, how to find x and y equation,